In software engineering interviews, algorithmic challenges are not just tests of coding proficiency but also assessments of problem-solving depth and adaptability.

Today, I'm delighted to explore one such intriguing problem from LeetCode: "Diameter of Binary Tree" (LeetCode 543). This problem provides a fascinating glimpse into binary trees, a cornerstone data structure in computer science, and tests our ability to understand and manipulate tree-based algorithms.

Introduction to the Problem

Imagine a binary tree, a structure where each node has up to two children. The "Diameter of Binary Tree" problem asks us to find the longest path between any two nodes in such a tree. This path, interestingly, may or may not pass through the tree's root, adding a layer of complexity to the challenge. The "length" of this path is quantified by the number of edges (connections) between these nodes.

For example, consider a binary tree where one branch is significantly longer than the other. Intuitively, the longest path might stretch from the furthest leaf of the longer branch, through the root, to the furthest leaf of the shorter branch. However, if both branches are long but one contains a "deeper" subtree, the longest path could entirely bypass the root, weaving through the nodes of this deeper subtree instead.

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

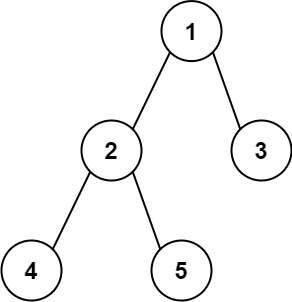
Example 1:

Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

The First Pass Implementation

Initially, one might approach this problem by simply calculating the sum of the maximum depths of the left and right subtrees of the root. This method hinges on the assumption that the longest path must pass through the root node.

def diameterOfBinaryTreeFirstPass(root: TreeNode) -> int:
    def depth(node: TreeNode) -> int:
        if not node:
            return 0
        return 1 + max(depth(node.left), depth(node.right))
    return depth(root.left) + depth(root.right)

This solution, while a good starting point, overlooks critical edge cases.

Understanding the Edge Case

The edge case arises when the longest path does not pass through the root. Consider a tree shaped like a 'Y'. The longest path might stretch from one leaf at the top of the 'Y', down the stem, and up the other branch, completely ignoring the root of the overall tree. This observation is crucial for developing a more accurate solution.

The Complete Solution

To fully address the problem, including its edge cases, we adopt a strategy that evaluates the diameter at every node. We maintain a global variable to track the maximum diameter found during traversal. Here's how we can implement this:

def diameterOfBinaryTree(root: TreeNode) -> int:
    diameter = 0

    def depth(node: TreeNode) -> int:
        nonlocal diameter  # Allows us to modify the outer variable
        if not node:
            return 0
        left_depth = depth(node.left)
        right_depth = depth(node.right)

        # Update the maximum diameter found so far
        diameter = max(diameter, left_depth + right_depth)

        # Return the depth to continue the traversal
        return 1 + max(left_depth, right_depth)

    depth(root)
    return diameter

This implementation leverages a helper function, depth, to compute the depth of each subtree while simultaneously updating the diameter. This dual-purpose function ensures efficiency and completeness in our solution.

Explaining the Big O Runtime

The runtime complexity of this solution is O(n), where n is the number of nodes in the binary tree. This efficiency stems from the fact that each node is visited exactly once during the depth-first search traversal. By computing both the depth and updating the diameter in a single pass, we optimize our algorithm to run in linear time relative to the size of the input tree.

Conclusion

In conclusion, the "Diameter of Binary Tree" problem on LeetCode serves as a brilliant exercise in understanding not just binary trees, but also in applying depth-first search in a nuanced and effective manner.

The transition from a first pass solution to a comprehensive strategy underscores the importance of considering all possible configurations in tree-based problems. For both seasoned and budding software engineers, mastering such challenges is a step towards sharpening one's algorithmic thinking, a crucial skill in the ever-evolving landscape of technology.

Thank you for joining me on this deep dive. Happy coding, and may your problem-solving journey be as rewarding as it is enlightening!