Mastering Cycle Detection in Linked Lists: A LeetCode Guide
Unlock efficient solutions to the classic cycle detection problem with our comprehensive tutorial.
In programming interviews, especially when facing questions from platforms like LeetCode, the ability to efficiently solve problems related to data structures is crucial.
Today, I'm delving into a classic problem that tests your understanding of linked lists and cycle detection: determining if a linked list has a cycle in it. The essence of the problem is simple yet intriguing.
Given the head of a linked list, we must decide whether any node in the list can be reached again by continuously following the next pointer, essentially forming a cycle.
Introduction to the Problem
This is LeetCode problem 141: Linked List Cycle.
Consider a linked list where each node points to the next node in the list. A cycle occurs if a node's next pointer points back to a previous node, creating a loop. For instance:
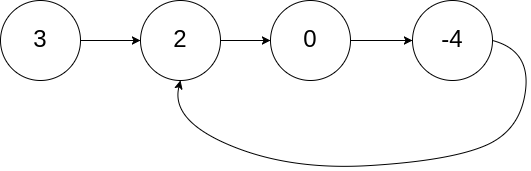
Example 1: Input:
head = [3,2,0,-4],pos = 1. The tail connects to the node at index 1 (0-indexed), forming a cycle. The expected output istrue.Example 2: Input:
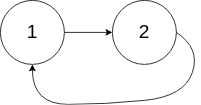
head = [1,2],pos = 0. Here, the tail connects back to the node at index 0, again indicating a cycle. The expected output istrue.Example 3: Input:
head = [1],pos = -1. In this case, the list does not have a cycle as there's only one node that doesn't point back to itself or another node. The expected output isfalse.
Dictionary/Set Solution
Description
One way to detect a cycle is by tracking nodes we've visited using a dictionary or set. As we traverse the linked list, we check if the current node is already in our set. If it is, we've found a cycle. Otherwise, we add the node to our set and continue.
This method has a time complexity of O(n), where n is the number of nodes in the linked list, since we potentially need to visit each node once. The space complexity is also O(n) because we store each node in a set.
Python Solution
# Definition for singly-linked list.
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def hasCycle(head: ListNode) -> bool:
visited = set()
while head:
if head in visited:
return True # Cycle detected
visited.add(head)
head = head.next
return False # No cycle found
Tortoise and Hare Solution
Description
The Tortoise and Hare algorithm is a two-pointer technique that uses two pointers moving at different speeds. It's a space-efficient way to detect cycles with a space complexity of O(1) - we only use two pointers, regardless of the list's size.
The time complexity remains O(n) because, in the worst case, the fast pointer might need to cycle through the list twice. The algorithm concludes there's a cycle if the fast pointer (hare) meets the slow pointer (tortoise).
Python Solution
def hasCycle(head: ListNode) -> bool:
if not head:
return False
slow, fast = head, head
while fast and fast.next:
slow = slow.next # Move slow pointer one step
fast = fast.next.next # Move fast pointer two steps
if slow == fast:
return True # Cycle detected
return False # No cycle found
Approaches in Other Languages
Solution in JavaScript
Here's how you can implement the Tortoise and Hare algorithm in JavaScript:
function hasCycle(head) {
if (!head) return false;
let slow = head;
let fast = head.next;
while (slow !== fast) {
if (!fast || !fast.next) return false;
slow = slow.next;
fast = fast.next.next;
}
return true;
}
Solution in Java
Here’s how you can implement the Tortoise and Hare algorithm in Java:
public boolean hasCycle(ListNode head) {
if (head == null) return false;
ListNode slow = head;
ListNode fast = head.next;
while (slow != fast) {
if (fast == null || fast.next == null) {
return false;
}
slow = slow.next;
fast = fast.next.next;
}
return true;
}
Comparison of Approaches
| Aspect | Dictionary/Set Approach | Tortoise and Hare Approach |
| Time Complexity | O(n) | O(n) |
| Space Complexity | O(n) | O(1) |
| Intuitive Understanding | Easy to grasp | Requires understanding of two-pointer techniques |
| Implementation Complexity | Straightforward | Slightly more complex but efficient |
Both methods offer solutions to the cycle detection problem, with the primary difference being the space complexity. The dictionary/set approach, while straightforward and easy to understand, uses more memory.
On the other hand, the Tortoise and Hare method is more space-efficient, making it a preferable choice in constraints environments or where large datasets are involved.
Conclusion
Mastering the art of cycle detection in linked lists not only prepares you for coding interviews but also sharpens your problem-solving skills.
With the detailed explanations and solutions provided, you're now better equipped to tackle this common yet challenging problem in various programming languages.