In the realm of software engineering interviews, the ability to tackle algorithm and data structure problems is a cornerstone of success. Today, I delve into the Height-Balanced Binary Tree problem (LeetCode 110 Balanced Binary Tree), a question that tests your understanding of binary trees and recursion—a common theme in coding interviews.

Let's embark on a journey to unravel this challenge, offering solutions and insights that cater to both experienced engineers and newcomers to the interview scene.

Introduction to the Problem

The Height-Balanced Binary Tree problem is a fundamental question that asks us to determine if a given binary tree is height-balanced. A binary tree is considered height-balanced if, for every node, the depth of the two subtrees never differs by more than one. For instance, consider the following examples:

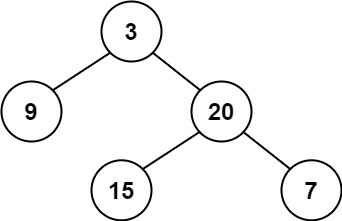
• Example 1: Input: root = [3,9,20,null,null,15,7] Output: true. This tree is balanced as the depths of the left and right subtrees of all nodes differ by no more than one.

  

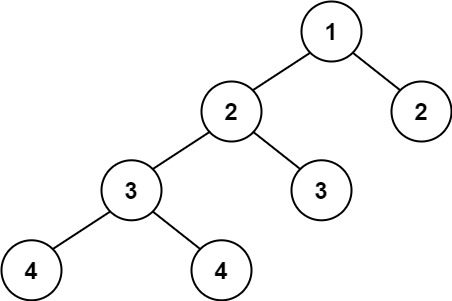
• Example 2: Input: root = [1,2,2,3,3,null,null,4,4] Output: false. This tree is not balanced because the depth difference between the left and right subtrees of the node with value 1 is more than one.

  

• Example 3: Input: root = [] Output: true. An empty tree is trivially balanced.

Solution Strategy

The essence of solving this problem lies in calculating the height of the subtrees for every node and ensuring the height difference does not exceed one. This can be achieved through a recursive depth-first search (DFS) strategy, which efficiently traverses the tree. The Big O notation for this algorithm is O(n), where n is the number of nodes in the tree. This is because each node is visited exactly once.

Python Solution Using Recursion

Here's a recursive solution in Python, which elegantly captures the essence of our strategy:

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def isBalanced(root: TreeNode) -> bool:
    def checkHeight(node):
        # Base case: An empty tree is height-balanced
        if not node:
            return 0
        left = checkHeight(node.left)
        right = checkHeight(node.right)
        # If left or right is unbalanced, or the height difference is > 1
        if left == -1 or right == -1 or abs(left - right) > 1:
            return -1  # Mark as unbalanced
        return 1 + max(left, right)  # Return the height of the tree rooted at `node`

    return checkHeight(root) != -1

This solution employs a helper function checkHeight that returns -1 if the subtree is unbalanced and otherwise returns its height. This dual-purpose approach minimizes the computational overhead and allows using boolean and number return types.

Understanding Postorder Traversal

Before delving into the Python solution using postorder traversal, let's briefly understand what it is. Postorder traversal is a way of traversing a binary tree where we first visit the left subtree, then the right subtree, and finally the node itself. This traversal method is particularly useful for problems where you need to visit children nodes before the parent, as it is in checking for a balanced binary tree.

Python Solution Using Post Order Traversal

This approach utilizes a non-recursive technique, leveraging a stack for traversal:

def isBalanced(root: Optional[TreeNode]) -> bool:
        stack = []
        node = root
        last = None
        depths = {}
        while stack or node:
            if node:
                stack.append(node)
                node = node.left
            else:
                node = stack[-1]
                if not node.right or last == node.right:
                    node = stack.pop()
                    left = depths.get(node.left, 0)
                    right = depths.get(node.right, 0)
                    if abs(left - right) > 1:
                        return False
                    depths[node] = 1 + max(left, right)
                    last = node
                    node = None
                else:
                    node = node.right
        return True

TypeScript Solution

The TypeScript solution mirrors the recursive Python solution with slight syntactical adjustments:

interface TreeNode {
    val: number;
    left: TreeNode | null;
    right: TreeNode | null;
}

function isBalanced(root: TreeNode | null): boolean {
    const checkHeight = (node: TreeNode | null): number => {
        if (node === null) return 0;
        const left = checkHeight(node.left);
        const right = checkHeight(node.right);
        if (left === -1 || right === -1 || Math.abs(left - right) > 1) return -1;
        return 1 + Math.max(left, right);
    };
    return checkHeight(root) !== -1;
};

Java Solution

Lastly, this Java solution also reflects the recursive approach:

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

public class Solution {
    private int checkHeight(TreeNode root) {
        if (root == null) return 0;
        int left = checkHeight(root.left);
        int right = checkHeight(root.right);
        if (left == -1 || right == -1 || Math.abs(left - right) > 1) return -1;
        return 1 + Math.max(left, right);
    }

    public boolean isBalanced(TreeNode root) {
        return checkHeight(root) != -1;
    }
}

Conclusion

Mastering the Height-Balanced Binary Tree problem is a significant step forward in your coding interview preparation journey. By understanding the recursive and iterative approaches to this problem, you're not only ready to tackle similar questions but also equipped with strategies that apply to a broader range of algorithm challenges. Whether you're an experienced engineer or new to coding interviews, these insights will help you approach binary tree problems with confidence.

Remember, the key to excelling in coding interviews is practice and understanding the underlying principles of data structures and algorithms. Happy coding!