Welcome to this installment of our software engineering interview tutorial series. Today, we're diving into a common yet intriguing problem often encountered on platforms like LeetCode: calculating the maximum depth of a binary tree (LeetCode 104. Maximum Depth of Binary Tree).

This challenge is not just about finding a solution; it's about understanding the intricacies of binary trees, recursion, and the implications of our approach on performance. Whether you're gearing up for interviews or honing your problem-solving skills, this guide will arm you with the knowledge and tools you need to excel.

Understanding the Problem

At its core, the problem asks us to determine the maximum depth (or height) of a binary tree, which is the number of nodes from the root down to the farthest leaf. Consider a tree with a single root node and two children; its depth is 2. But, if one child has its own child, the tree's depth becomes 3.

Examples:

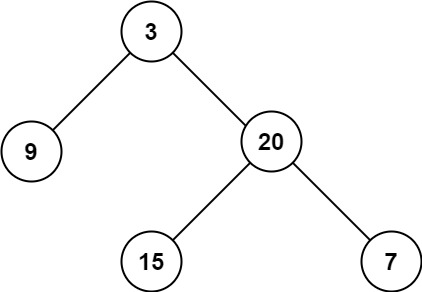
• For a tree structure [3,9,20,null,null,15,7], the maximum depth is 3.

• A tree like [1,null,2] has a depth of 2, illustrating a lean, imbalanced tree but still showcasing the need to accurately assess depth.

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Strategy for Solution

To solve this problem, we employ recursion, a fundamental concept in computer science where a function calls itself with a subset of the original problem. The beauty of recursion in this context lies in its ability to elegantly traverse the tree, depth-first, ensuring we reach every leaf and calculate the depth along the way.

The process is straightforward:

• If the current node (root) is None, the depth is 0 since we've hit the base case of an empty tree.

• Otherwise, we recursively calculate the depth of the left and right subtrees and take the maximum of both, adding 1 to account for the current node's depth.

Big O Analysis

The time complexity is O(n), where n is the number of nodes in the tree. This is because we must visit each node exactly once to determine the depth. The space complexity is O(h), where h is the height of the tree, due to the recursion stack.

Solution in Python

Let's look at the Python solution, noting how recursion plays a pivotal role:

class TreeNode:
    def maxDepth(root: Optional[TreeNode]) -> int:
        if root is None:
            return 0
        # Recursively find the depth of left and right subtrees, and take the max
        return max(1 + maxDepth(root.left), 1 + maxDepth(root.right))

Solution in TypeScript

Translating our approach to TypeScript, we maintain the same logic while adapting to the syntax and type definitions of TypeScript:

function maxDepth(root: TreeNode | null): number {
    if (root === null) {
        return 0;
    }
    return Math.max(1 + maxDepth(root.left), 1 + maxDepth(root.right));
}

Solution in Java

Lastly, our Java solution also mirrors the recursive strategy, showcasing the universal applicability of our approach:

public int maxDepth(TreeNode root) {
    if (root == null) {
        return 0;
    }
    return Math.max(1 + maxDepth(root.left), 1 + maxDepth(root.right));
}

Conclusion

Mastering the "Maximum Depth of Binary Tree" problem not only boosts your interview readiness but also deepens your understanding of binary trees and recursion.

The cross-language solutions provided illustrate the problem's fundamental nature, transcending specific programming languages. Dive into the code, experiment with it, and remember that the journey of mastering data structures and algorithms is a marathon, not a sprint.

Happy coding!