In today's blog post, I want to walk you through a classic problem that often surfaces in software engineering interviews, particularly on platforms like LeetCode. The problem in question is known as "Flood Fill" (LeetCode 733), a concept that finds its roots in graphics editing software but has broader applications in areas such as game development and data analysis.

Let's embark on a journey to unravel the intricacies of this problem, explore various strategies to tackle it, and, most importantly, understand the underlying principles that can be applied to a wide range of coding challenges.

Introduction to Flood Fill

Imagine you're working with a digital image represented as a 2D grid, where each cell contains a pixel's color value. Given coordinates (sr, sc) in this grid, along with a new color value, your task is to change the color of the specified pixel and all adjacent pixels that share the original color to the new color. This process should continue spreading to further pixels that are 4-directionally connected and share the same original color, resembling a "flood" of color filling an area of the image.

An image is represented by an m x n integer grid imagewhere image[i][j] represents the pixel value of the image.

You are also given three integers sr, sc, and color. You should perform a flood fill on the image starting from the pixel image[sr][sc].

To perform a flood fill, consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, plus any pixels connected 4-directionally to those pixels (also with the same color), and so on. Replace the color of all of the aforementioned pixels with color.

Return the modified image after performing the flood fill.

Example 1:

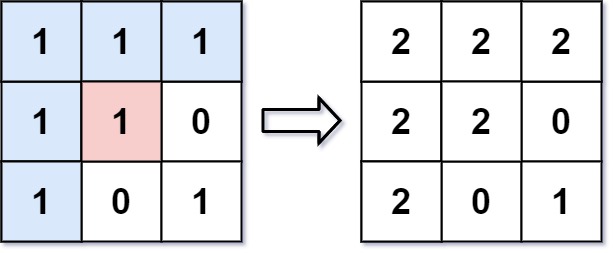
Input: image = [[1,1,1],[1,1,0],[1,0,1]], sr = 1, sc = 1, color = 2
Output: [[2,2,2],[2,2,0],[2,0,1]]
Explanation: From the center of the image with position (sr, sc) = (1, 1) (i.e., the red pixel), all pixels connected by a path of the same color as the starting pixel (i.e., the blue pixels) are colored with the new color.
Note the bottom corner is not colored 2, because it is not 4-directionally connected to the starting pixel.

Example 2:

Input: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, color = 0
Output: [[0,0,0],[0,0,0]]
Explanation: The starting pixel is already colored 0, so no changes are made to the image.

Considering Different Approaches

When faced with the Flood Fill problem, two primary approaches come to mind: Depth-First Search (DFS) and Breadth-First Search (BFS). Both strategies are viable for exploring the image grid and updating the necessary pixels.

• DFS involves diving as deep as possible into one direction before backtracking, which is particularly efficient in this case due to the recursive nature of the color fill.

• BFS, on the other hand, explores neighbors of all the nodes at the present depth before moving on to the nodes at the next depth level.

While BFS can also solve the problem, it generally requires more memory than DFS since it keeps track of all the nodes at a given depth.

The Solution Explained

I prefer using the DFS approach for its elegance and simplicity in implementation. The idea is to start from the given pixel (sr, sc), check if it's within the bounds of the image and if it matches the original color (to avoid infinite recursion). If it does, we change its color to the new one and recursively apply the same process to its 4-directional neighbors (up, down, left, right).

Recursion Steps

1. Starting Point: The DFS begins from the pixel specified by sr (starting row) and sc (starting column). This is the root of our DFS traversal.

2. Recursive Exploration: From the starting pixel, the algorithm recursively explores each of the 4-directional neighbors. For each neighbor, it checks if the neighbor is within the bounds of the image, if it has not already been filled with the new color, and if it matches the original color of the starting pixel. If all these conditions are met, the algorithm fills the neighbor with the new color and recursively applies the same process to its neighbors.

3. Base Conditions: The recursion has several base conditions to stop further exploration:

   • If the pixel is out of the image's bounds.

   • If the pixel's color is different from the original color (indicating it's either already been filled or it was never part of the connected component we're filling).

   • If the pixel is already the new color (to prevent infinite recursion).

4. Backtracking: Once all valid 4-directional neighbors of a pixel have been explored and filled, the DFS backtracks to explore other paths, eventually filling all connected pixels of the original color with the new color.

Big O Analysis

The complexity of this operation is O(n), where n is the number of pixels in the image, as in the worst case, we might need to visit each pixel once.

Python Solution

class Solution:
    def fill(self, image, sr, sc, color, cur):
        # Check bounds and if current pixel matches the target color
        if sr < 0 or sr >= len(image) or sc < 0 or sc >= len(image[0]) or cur != image[sr][sc]:
            return

        # Update the color of the current pixel
        image[sr][sc] = color

        # Recursively fill 4-directionally
        self.fill(image, sr-1, sc, color, cur) # Up
        self.fill(image, sr+1, sc, color, cur) # Down
        self.fill(image, sr, sc-1, color, cur) # Left
        self.fill(image, sr, sc+1, color, cur) # Right

    def floodFill(self, image, sr, sc, color):
        # If the color of the starting pixel is already the target color, no need to proceed
        if image[sr][sc] == color: return image

        # Begin the flood fill process
        self.fill(image, sr, sc, color, image[sr][sc])
        return image

This solution elegantly captures the essence of the Flood Fill algorithm, with comments added for clarity. The fill method is a helper that performs the DFS, ensuring that we only paint pixels that match the original color, thereby preventing infinite loops.

Conclusion

Solving the Flood Fill problem not only tests your ability to navigate 2D arrays but also your understanding of recursive algorithms and graph traversal techniques. Through this exercise, we've seen how a seemingly simple problem can offer deep insights into algorithm design and optimization.

Whether you're preparing for your next software engineering interview or just looking to sharpen your coding skills, mastering problems like Flood Fill on LeetCode is a step in the right direction.

Remember, the key to excelling in coding interviews is not just solving the problem but understanding the principles behind your solution. Happy coding!